

Even without the unit, you should be able to get a lot of good ideas for teaching dividing with area models and partial quotient. All of the printables shown in this post are from my division unit. We want students to grasp the how and why of what they are doing and to become flexible in their thinking.
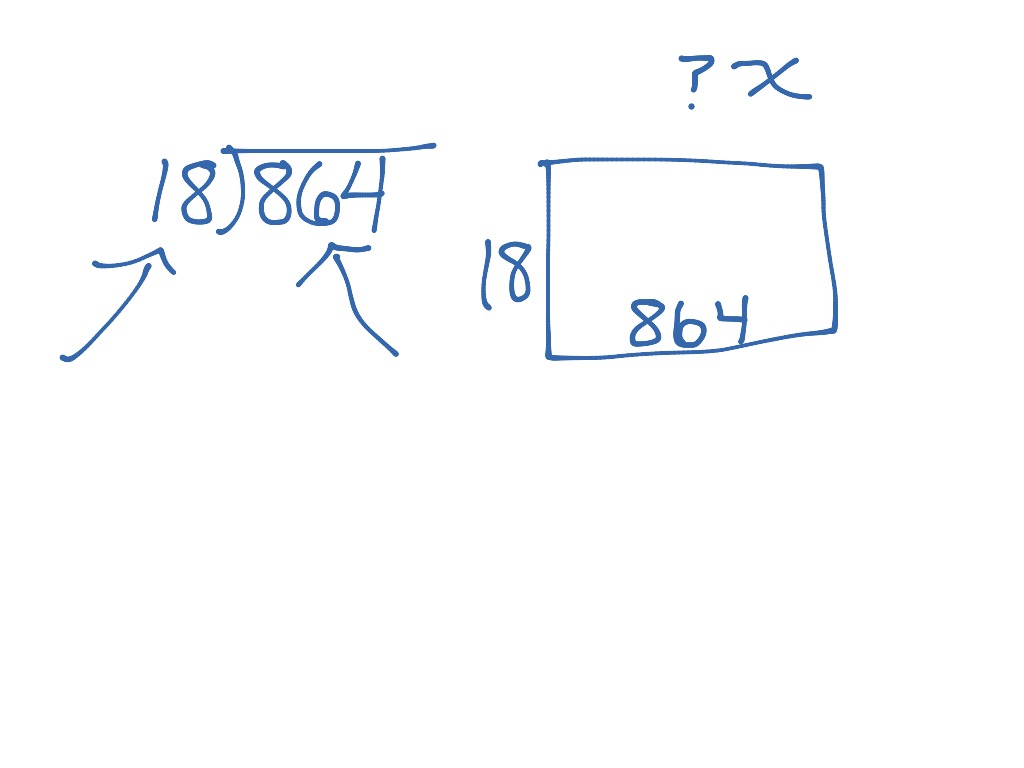
#Area models for division series#
When teaching dividing with area models and partial quotient, we don’t want the strategies to be a series of steps for students to follow without any real meaning. If you want to see how I teach multi-digit multiplication, be sure to check out this blog post. In this post, I’ll keep the focus on multi-digit division.įor students to fully understand multi-digit division, they have to understand the concept of multiplication. You can read more about the value of teaching both concepts and procedures here. As a student, I only understood procedures. One of the reasons dividing with area models and partial quotient was confusing for me is that I had not learned multi-digit multiplication or division conceptually. Hopefully, this post will save you the headaches I experienced learning this important concept. All of a sudden, the pieces fell into place, and it all made sense.
#Area models for division how to#
Confession: when I first moved to fourth grade, I had no clue how to divide with an area model or partial quotient! After teaching it to myself, I hated it! Dividing with area models and partial quotient didn’t click for me until I was actually teaching my class. What fraction is represented by the intersection of the two shaded areas? 6/12.Dividing with area models and partial quotient is a major part of fourth grade standards.
Next, divide the unit square horizontally into fourths. To demonstrate this with an area model, begin by dividing the unit square vertically into thirds. Let's take a look at a multiplication problem: 2/3 x 3/4. What is the new fraction represented by the shaded area? 8/12. Next, divide the area of the unit square into four horizontal rectangles (to demonstrate that you're multiplying both the numerator and denominator by 4). Shade in 2/3 of the area of the unit square. If we were to demonstrate 2/3 = 8/12 fact using an area model, first divide the area of the unit square into three rectangles. If your students are ready to be challenged with the symbolic form, you can explain: After various opportunities to experiment informally with fraction sticks and write down their observations, they will be ready to learn a more formal rule: when you multiply the numerator and denominator by the same non-zero number, you will obtain an equivalent fraction. They can choose a fraction, such as 2/3, and see what combinations of other fractions are equivalent, such as 8/12. This is a great time for students to experiment informally with fraction sticks. So, let’s talk about finding equivalent fractions!

Understanding equivalent fractions is important when comparing and ordering fractions, adding and subtracting fractions with unlike denominators, and reducing fractions to their lowest term. Here are some math concepts you can model with fraction sticks and area models:Ī prevalent theme in the Grade 4 Common Core standards is understanding equivalent fractions, or, more precisely, the notion that a fraction remains the same when you multiply the numerator and denominator by a non-zero whole number. An area model is a square that you divide into equal-sized rectangles to represent a fraction. An area model is a useful tool you can use to model certain fraction concepts.


 0 kommentar(er)
0 kommentar(er)
